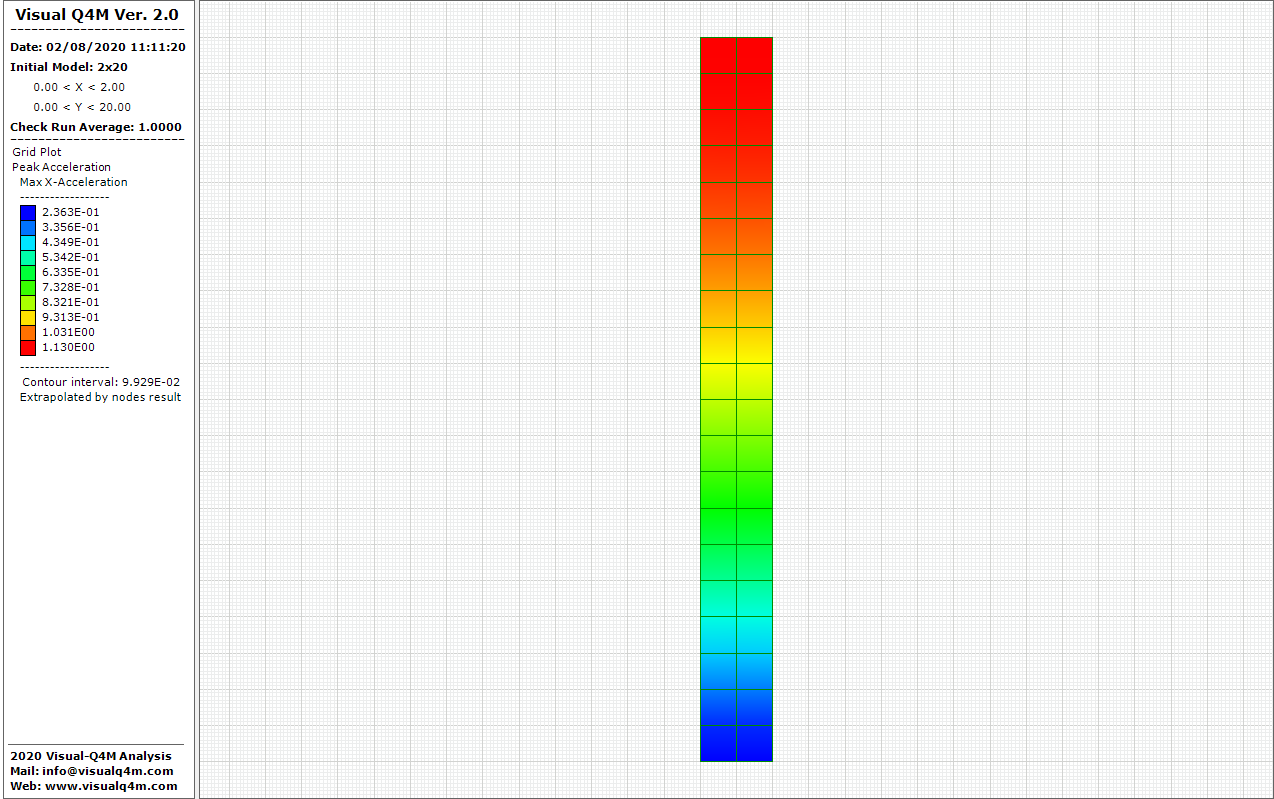
Problems solving 1D: Natural Frequency
A column of elastic material (single-lithology) resting on a rigid base has natural periods of vibration that depend on the mode of oscillation. The theoretical value for natural frequency of oscillation (f) is given by:
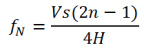
where:
- H = column height of soil (for this verification H=20.0 m)
- Vs = velocity of shear waves (for this verification Vs=100 m/s)
- fN = natural frequency of oscillation (for this verification fN=1.250 Hz)
- n = 1 (first mode shape)
Geometry and Material Properties
The model is a column whit dimension 2.0x20.0 meters and it composed of forty (40) regular elements and sixty-three (63) nodes.

Material Properties
| Density | Wave Vs | Shear Modulus | Poisson Ratio | Damping |
|---|---|---|---|---|
| 10 N/m2 | 100 m/s | 1.019E4 N/m2 | 0.10 | 1.0% |
Boudary Conditions
The column have a behavior in shear and the vertical motion (Y) is inhibited to eliminate bending modes. The loading is applied to the base (XY).

You apply the load horizontal component only in the nodes with X-Direction locked:
- Node 1, 1 --> Fix XY-Direction
- Node 2, 1 --> Fix XY-Direction
- Node 3, 1 --> Fix XY-Direction
Input Motion
For the estimation of the natural frequency of the system it is not important what kind of input motion it's used. The value is define only from mass matrix and stiffness matrix. Quad4M calculate the first angular frequency by solving the following system of equations:

Results
To the first iteration Visual-Q4M calculate the fundamental Frequency of the model and it's show the value in run window.

The minimal Angular Frequency = 7.851 [s^(-1)]
The calculated Natural Frequency fN = 1.250 [Hz]
The value of natural frequency change if it's modified the mass and/or stiffness of the model.