Problems solving 1D: Equivalent Liner Analysis
A column of elastic material (single-lithology) resting on a rigid base has natural periods of vibration that depend on the mode of oscillation. The theoretical value for natural frequency of oscillation (f) is given by:
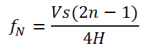
where:
- H = column height of soil (for this verification H=100.0 m);
- Vs = average velocity of shear waves
| Layer | Thickness | Wave Vs |
|---|---|---|
| 1 | 2.0 | 141 |
| 2 | 2.0 | 224 |
| 3 | 2.0 | 267 |
| 4 | 7.5 | 292 |
| 5 | 2.0 | 355 |
| 6 | 9.5 | 406 |
| 7 | 55.0 | 485 |
| 8 | 20.0 | 546 |
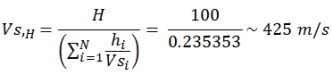
The calculated Natural Frequency is 1.063Hz equal to 0.940s of Period.
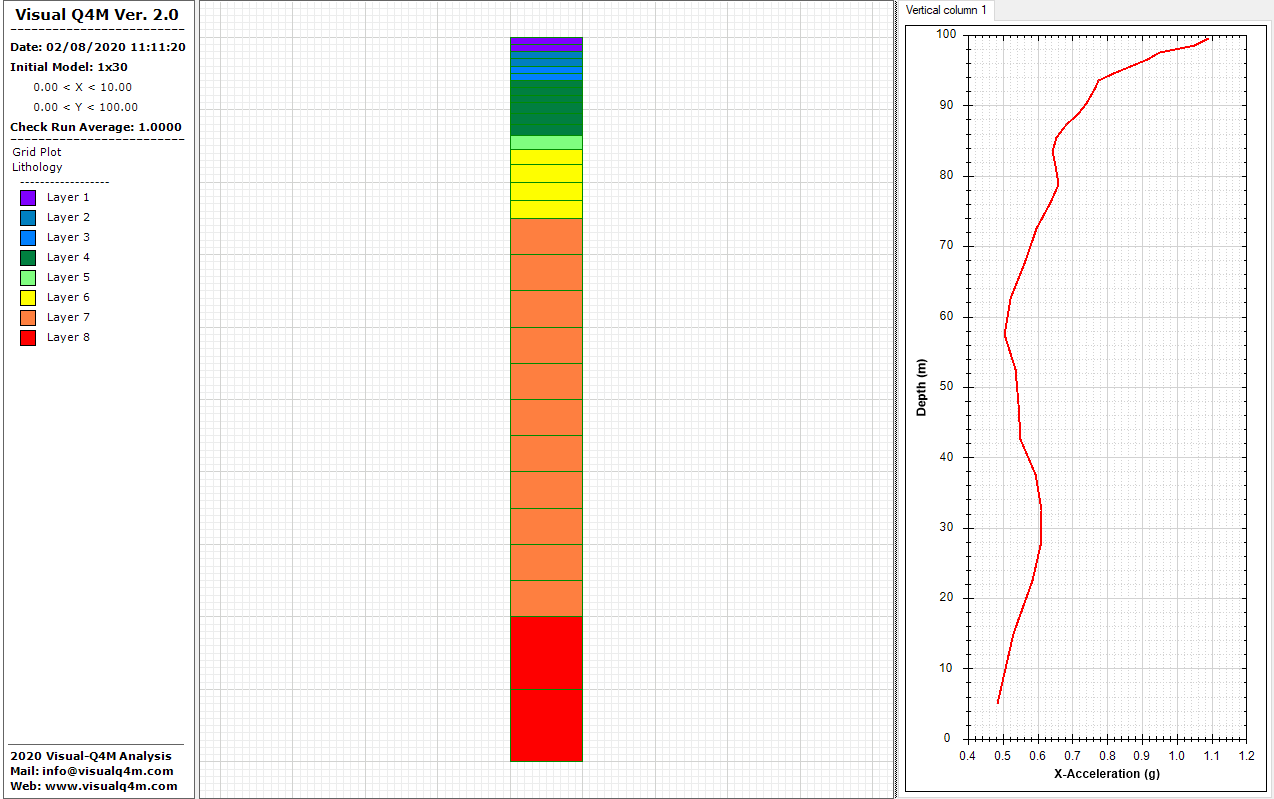
Geometry and Material Properties
The model is a column with dimension 100.0x10.0 meters and it make of thirty (30) elements and sixty-two (62) nodes. The elements have varying heights depending on the thickness of the layer (Height Min = 1.0m, Height Max = 10.0m).
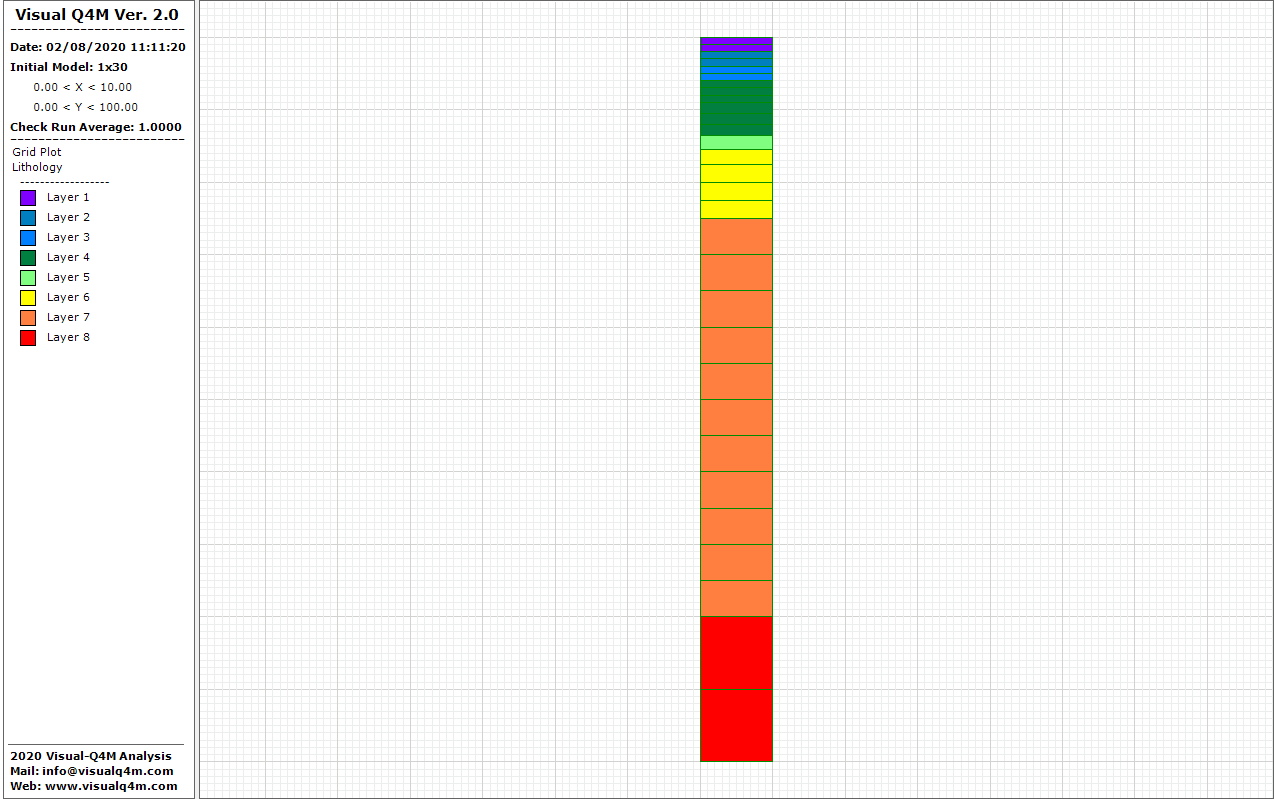
Material Properties
| Layer | Density | Wave Vs | Shear Modulus | Poisson Ratio | Damping | G/G0 - D% |
|---|---|---|---|---|---|---|
| 1 | 19710 N/m2 | 141 m/s | 2.796E7 N/m2 | 0.45 | 5.0 % | Soil 1 |
| 2 | 19710 N/m2 | 224 m/s | 7.057E7 N/m2 | 0.45 | 5.0 % | Soil 1 |
| 3 | 19710 N/m2 | 267 m/s | 1.003E8 N/m2 | 0.45 | 5.0 % | Soil 1 |
| 4 | 18460 N/m2 | 292 m/s | 1.123E8 N/m2 | 0.45 | 5.0 % | Soil 2 |
| 5 | 18460 N/m2 | 355 m/s | 1.660E8 N/m2 | 0.45 | 5.0 % | Soil 2 |
| 6 | 18060 N/m2 | 406 m/s | 2.124E8 N/m2 | 0.45 | 5.0 % | Soil 3 |
| 7 | 19000 N/m2 | 485 m/s | 3.189E8 N/m2 | 0.45 | 5.0 % | Soil 4 |
| 8 | 20000 N/m2 | 567 m/s | 4.254E8 N/m2 | 0.45 | 5.0 % | Soil 4 |
-
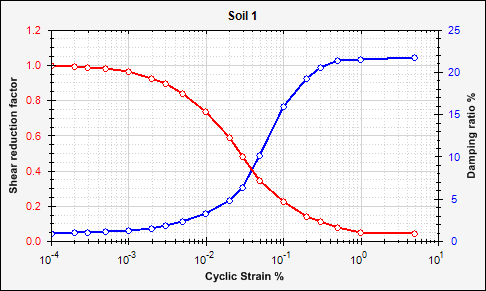
- Curve Soil 1
-
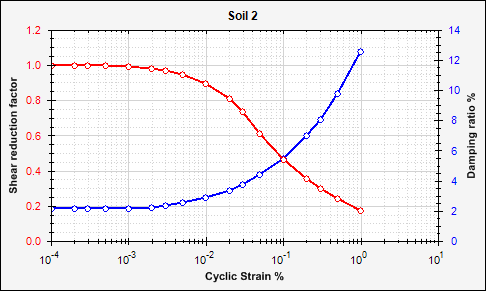
- Curve Soil 2
-
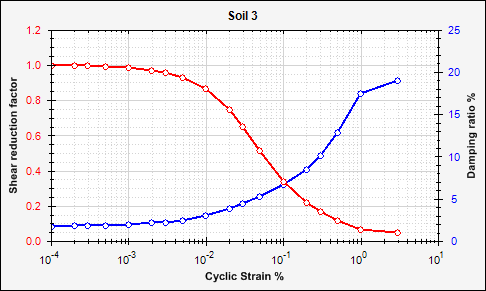
- Curve Soil 3
-
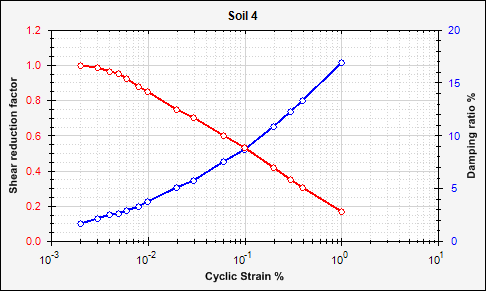
- Curve Soil 4
Boudary Conditions
The column have a behavior in shear and the vertical motion (Y) is inhibited to eliminate bending modes. The loading is applied to the base (XY). You apply the load horizontal component only in the nodes with X-Direction locked:
- Node 1, 1 --> Fix XY-Direction
- Node 1, 2 --> Fix XY-Direction
Input Motion
The horizontal acceleration is Kobe FN SSE where:
- Records = 8000
- Time = 44.0 sec
- Time step = 0.005 sec
- PGA = 0.942 g
Results
To the first iteration, Visual-Q4M calculate the fundamental Frequency of model and it is show the value in run window.
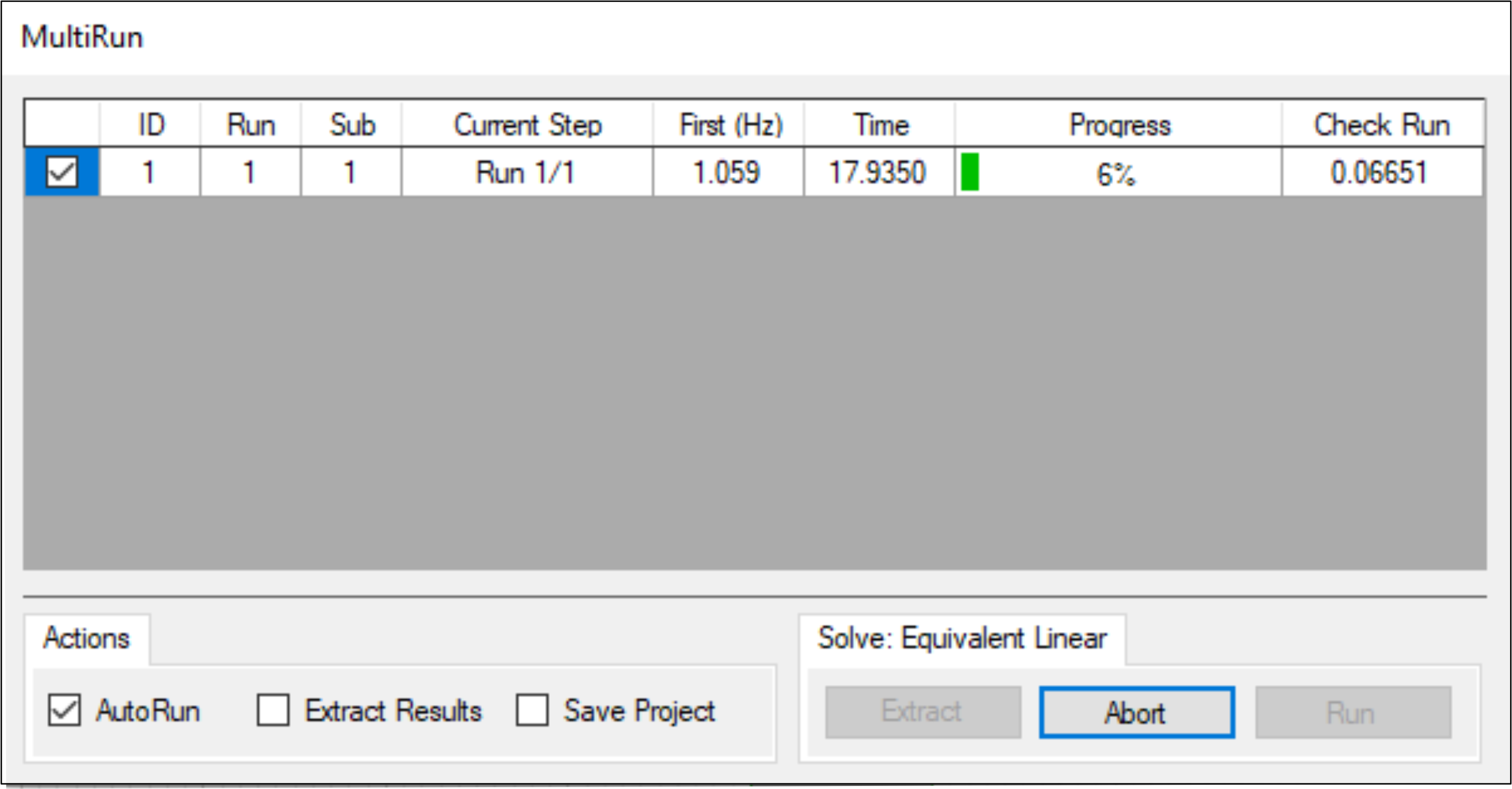
The minimal Angular Frequency = 6.651 [s^(-1)]
The calculated Natural Frequency fN = 1.059 [Hz]
The value of natural frequency change if the stiffness of the model is modified. In calculation cycles (Max Run: 20) both the value of strain and the corresponding G/G0 and D% on variation curve is calculated.

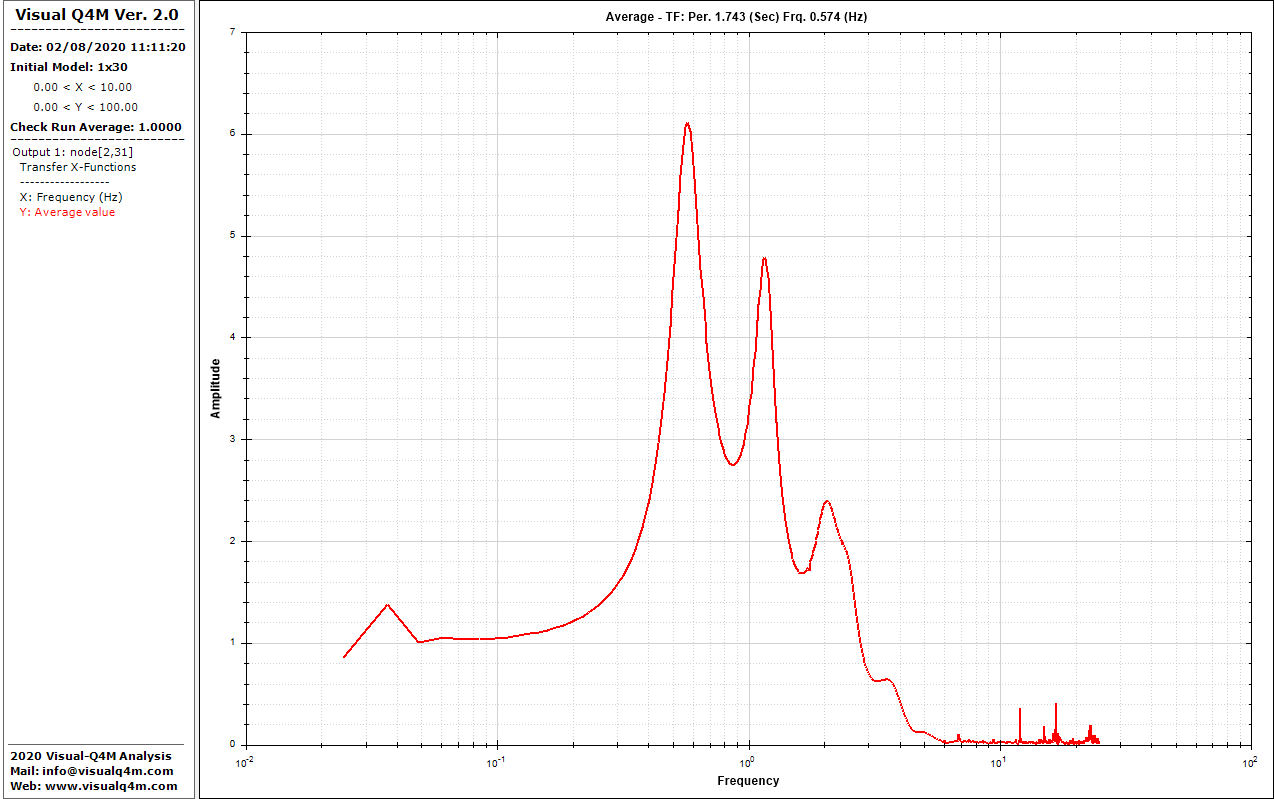
The figures show the horizontal transfer function at the top of the column (node 2,31) with a predominant frequency of 0.623 Hz.